JavaScript is required
Back

堆排序

Sep 12, 2023
#排序 #数据结构与算法

堆排序

堆排序（Heap Sort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法：

  • 大顶堆：每个节点的值都大于或等于其子节点的值，在堆排序算法中用于升序排列；
  • 小顶堆：每个节点的值都小于或等于其子节点的值，在堆排序算法中用于降序排列；

算法原理

  1. 先将初始的 Heap[0...n-1] 建立成最大堆，此时是无序堆，而堆顶是最大元素
  2. 再将堆顶 Heap[0] 和无序区的最后一个记录 Heap[n-1] 交换，由此得到新的 无序区 Heap[0...n-2] 和 有序区 Heap[n-1]，且满足 Heap[0...n-2].keys <= Heap[n-1].key
  3. 由于交换后新的根 Heap[1] 可能违反堆性质，故应将当前无序区 Heap[1..n-1] 调整为堆。然后再次将 Heap[1..n-1] 中关键字最大的记录 Heap[1] 和该区间的最后一个记录 Heap[n-1] 交换，由此得到新的无序区 Heap[1..n-2] 和有序区 Heap[n-1..n]，且仍满足关系 Heap[1..n-2].keys≤R[n-1..n].keys，同样要将 Heap[1..n-2] 调整为堆。
  4. 直到无序区只有一个元素为止。

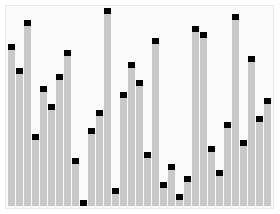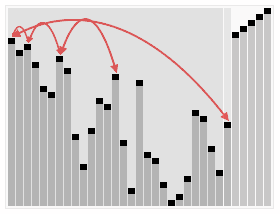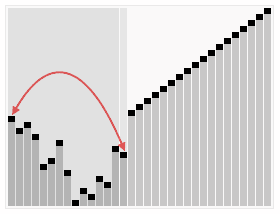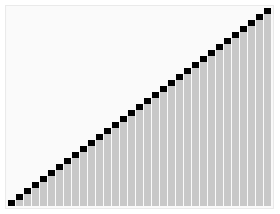
算法实现

function heapSort(arr) {
  // 建堆
  let size = arr.length
  for (let i = Math.floor(size / 2) - 1; i >= 0; i--) {
    heapify(arr, i, size)
  }

  // 堆排序
  for (let j = size - 1; j >= 1; j--) {
    // 堆数组中首个元素为值最大元素，与末尾元素交换
    ;[arr[0], arr[j]] = [arr[j], arr[0]]
    // 交换后，再将堆数组中未排序部分进行堆化
    // 堆化后首个元素又是未排序部分的最大值，下次循环再次交换
    heapify(arr, 0, --size)
  }

  return arr
}

// 自上而下堆化
function heapify(arr, index, len) {
  let leftIndex = 2 * index + 1,
    rightIndex = 2 * index + 2,
    largest = index

  // 左子节点比当前子节点大，则记录左子节点为比较大的节点
  if (leftIndex < len && arr[leftIndex] > arr[largest]) {
    largest = leftIndex
  }

  // 右子节点比当前子节点大，则记录右子节点为比较大的节点
  if (rightIndex < len && arr[rightIndex] > arr[largest]) {
    largest = rightIndex
  }

  // 最大的节点为非当前字节时
  if (largest != index) {
    // 上下交换节点
    ;[arr[index], arr[largest]] = [arr[largest], arr[index]]
    heapify(arr, largest, len)
  }
}

参考资料